Jump-diffusion processes¶

We will show here how to: (1) generate trajectories of jump-diffusion processes; (2) retrieve the parameters from a single trajectory of a jump-diffusion process. Naturally, if we already had some data – maybe from a real-world recording of a stochastic process – we would simply look at estimating the parameters for this process.

The theory¶

Jump-diffusion processes¹, as the name suggest, are a mixed type of stochastic processes with a diffusive and a jump term. One form of these processes which is mathematically traceable is given by the Stochastic Differential Equation

\[\mathrm{d} X(t) = a(x,t)\;\mathrm{d} t + b(x,t)\;\mathrm{d} W(t) + \xi\;\mathrm{d} J(t),\]

which has four main elements: a drift term \(a(x,t)\), a diffusion term \(b(x,t)\), linked with a Wiener process \(W(t)\), a jump amplitude term \(\xi(x,t)\), which is given by a Gaussian distribution \(\mathcal{N}(0,\sigma_\xi^2)\) coupled with a jump rate \(\lambda\), which is the rate of the Poissonian jumps \(J(t)\). You can find a good review on this topic in Ref. 2.

Integrating a jump-diffusion process¶

Let us use the functions in jumpdiff to generate a jump-difussion process, and subsequently retrieve the parameters. This is a good way to understand the usage of the integrator and the non-parametric retrieval of the parameters.

First we need to load our library. We will call it jd

import jumpdiff as jd

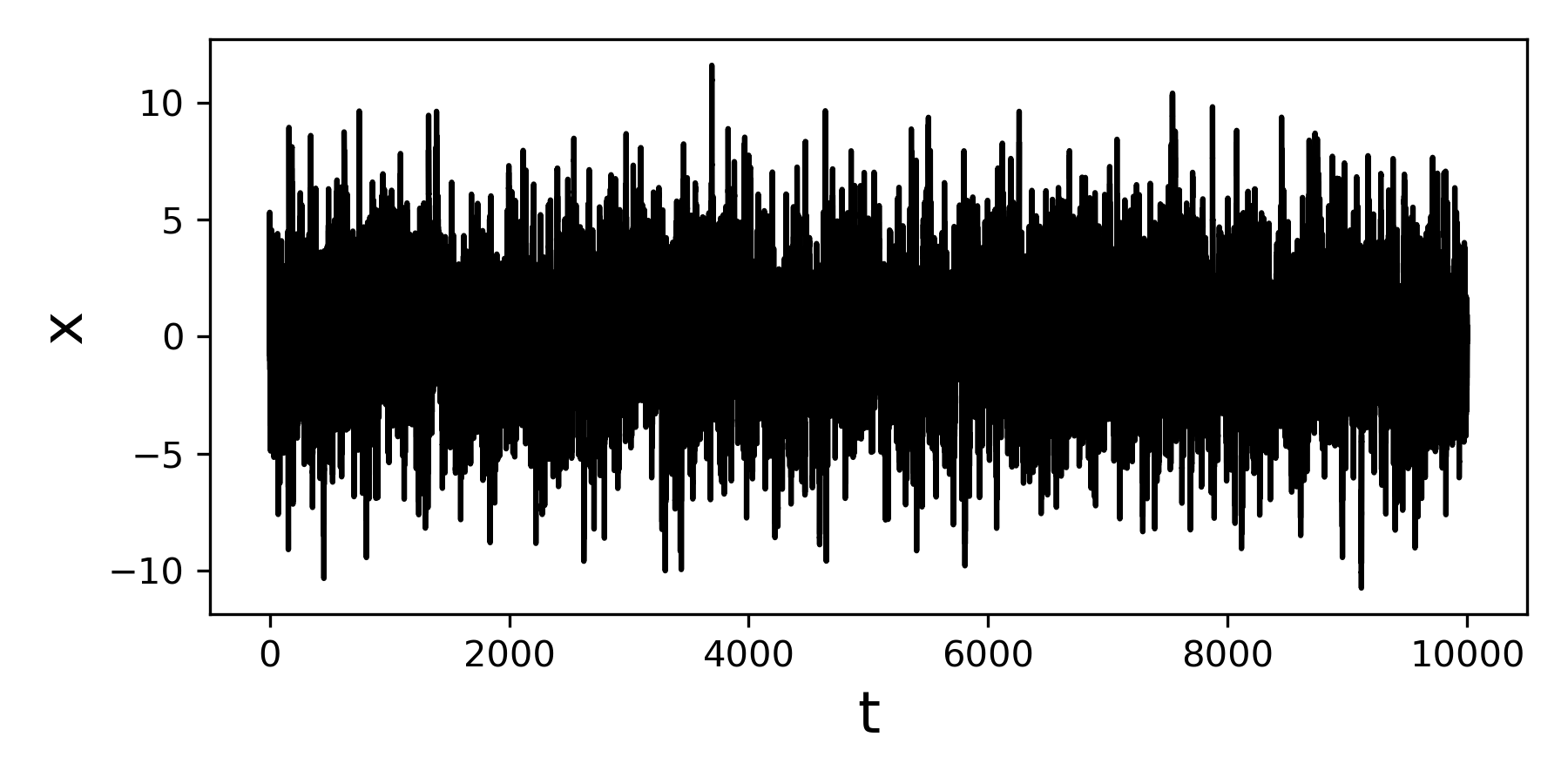
Let us thus define a jump-diffusion process and use jd_process to integrate it. Do notice here that we need the drift \(a(x,t)\) and diffusion \(b(x,t)\) as functions.

# integration time and time sampling
t_final = 10000
delta_t = 0.001

# A drift function
def a(x):
    return -0.5*x

# and a (constant) diffusion term
def b(x):
    return 0.75

# Now define a jump amplitude and rate
xi = 2.5
lamb = 1.75

# and simply call the integration function
X = jd.jd_process(t_final, delta_t, a=a, b=b, xi=xi, lamb=lamb)

This will generate a jump diffusion process X of length int(10000/0.001) with the given parameters.

Using `jumpdiff` to retrieve the parameters¶

Moments and Kramers─Moyal coefficients¶

Take the timeseries X and use the function moments to retrieve the conditional moments of the process. For now let us focus on the shortest time lag, so we can best approximate the Kramers—Moyal coefficients. For this case we can simply employ

edges, moments = jd.moments(timeseries = X)

In the array edges are the limits of our space, and in our array moments are recorded all 6 powers/order of our conditional moments. Let us take a look at these before we proceed, to get acquainted with them.

We can plot the first moment with any conventional plotter, so lets use here plotly from matplotlib. To visualise the first moment, simply use

import matplotlib.pyplot as plt
plt.plot(edges, moments[1]/delta_t)

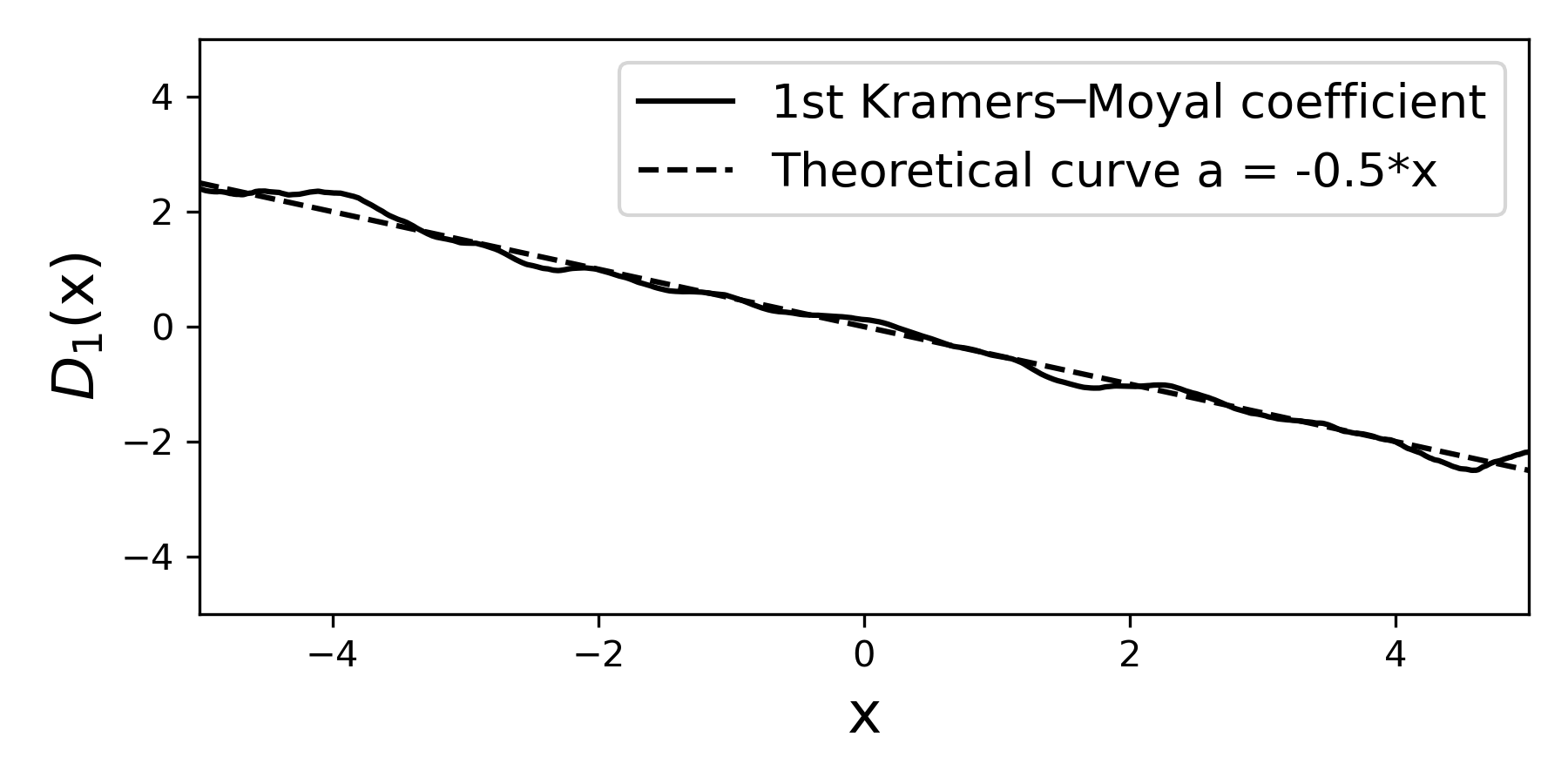
The first moment here (i.e., the first Kramers—Moyal coefficient) is given solely by the drift term that we have selected -0.5*x. In the plot we have also included the theoretical curve, which we know from having selected the value of a(x) in line 8.

Similarly, we can extract the second moment (i.e., the second Kramers—Moyal coefficient) is a mixture of both the contributions of the diffusive term \(b(x)\) and the jump terms \(\xi\) and \(\lambda\).

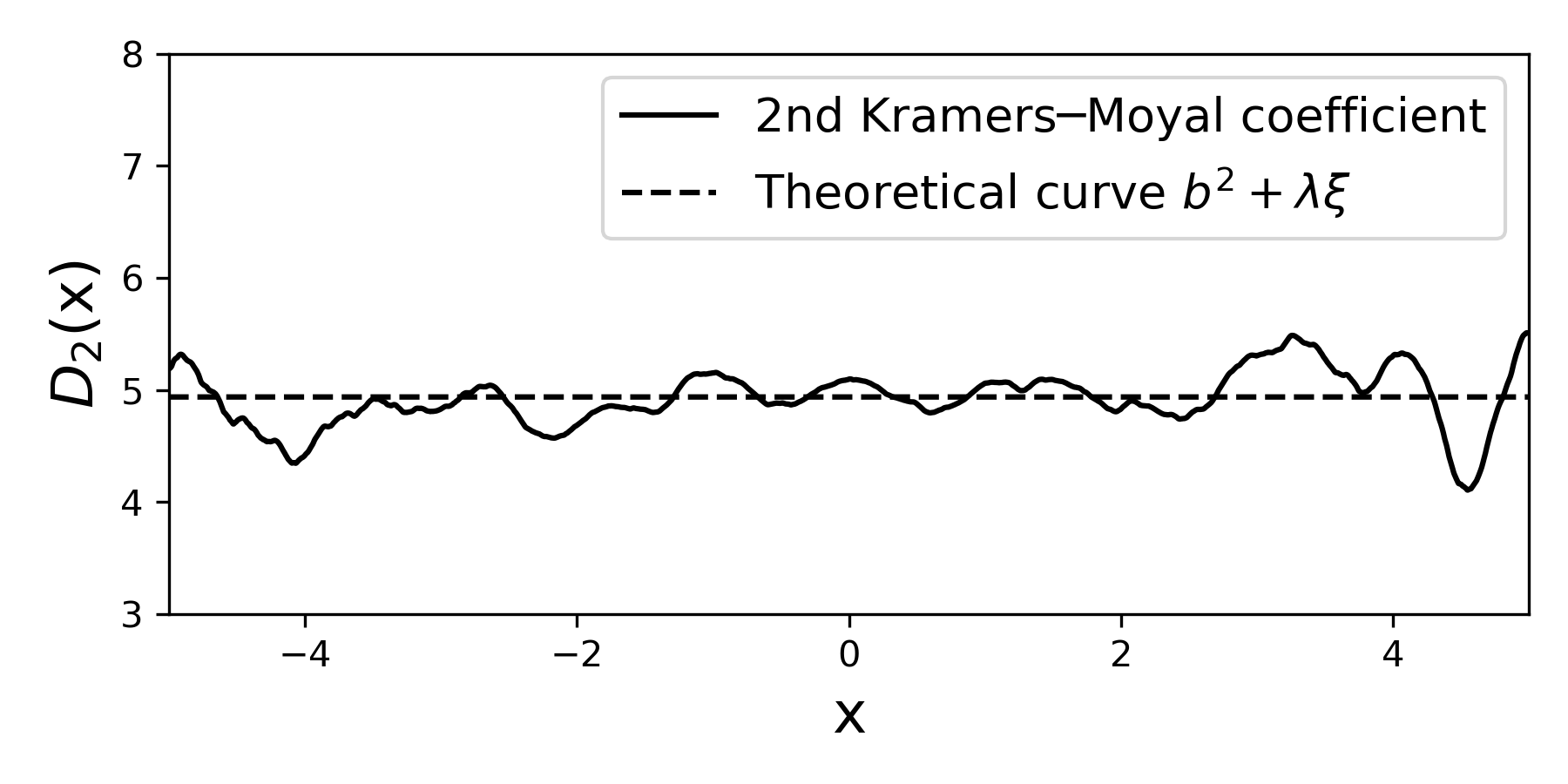
You have this stored in moments[2].

Jump-diffusion processes¶

The theory¶

Integrating a jump-diffusion process¶

Using jumpdiff to retrieve the parameters¶

Moments and Kramers─Moyal coefficients¶

Retrieving the jump-related terms¶

Using `jumpdiff` to retrieve the parameters¶