jumpdiff¶
jumpdiff is a python library with non-parametric Nadaraya—Watson estimators to extract the parameters of jump-diffusion processes.
With jumpdiff one can extract the parameters of a jump-diffusion process from one-dimensional timeseries, employing both a kernel-density estimation method combined with a set on second-order corrections for a precise retrieval of the parameters for short timeseries.
Installation¶
To install jumpdiff simply use
pip install jumpdiff
Then on your favourite editor just use
import jumpdiff as jd
The library depends on numpy, scipy, and sympy.
Jump-diffusion processes¶
We will show here how to: (1) generate trajectories of jump-diffusion processes; (2) retrieve the parameters from a single trajectory of a jump-diffusion process. Naturally, if we already had some data – maybe from a real-world recording of a stochastic process – we would simply look at estimating the parameters for this process.
The theory¶
Jump-diffusion processes1, as the name suggest, are a mixed type of stochastic processes with a diffusive and a jump term. One form of these processes which is mathematically traceable is given by the Stochastic Differential Equation
which has four main elements: a drift term \(a(x,t)\), a diffusion term \(b(x,t)\), linked with a Wiener process \(W(t)\), a jump amplitude term \(\xi(x,t)\), which is given by a Gaussian distribution \(\mathcal{N}(0,\sigma_\xi^2)\) coupled with a jump rate \(\lambda\), which is the rate of the Poissonian jumps \(J(t)\). You can find a good review on this topic in Ref. 2.
Integrating a jump-diffusion process¶
Let us use the functions in jumpdiff to generate a jump-difussion process, and subsequently retrieve the parameters. This is a good way to understand the usage of the integrator and the non-parametric retrieval of the parameters.
First we need to load our library. We will call it jd
1 | import jumpdiff as jd |
Let us thus define a jump-diffusion process and use jd_process to integrate it. Do notice here that we need the drift \(a(x,t)\) and diffusion \(b(x,t)\) as functions.
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | # integration time and time sampling t_final = 10000 delta_t = 0.001 # A drift function def a(x): return -0.5*x # and a (constant) diffusion term def b(x): return 0.75 # Now define a jump amplitude and rate xi = 2.5 lamb = 1.75 # and simply call the integration function X = jd.jd_process(t_final, delta_t, a=a, b=b, xi=xi, lamb=lamb) |
This will generate a jump diffusion process X of length int(10000/0.001) with the given parameters.
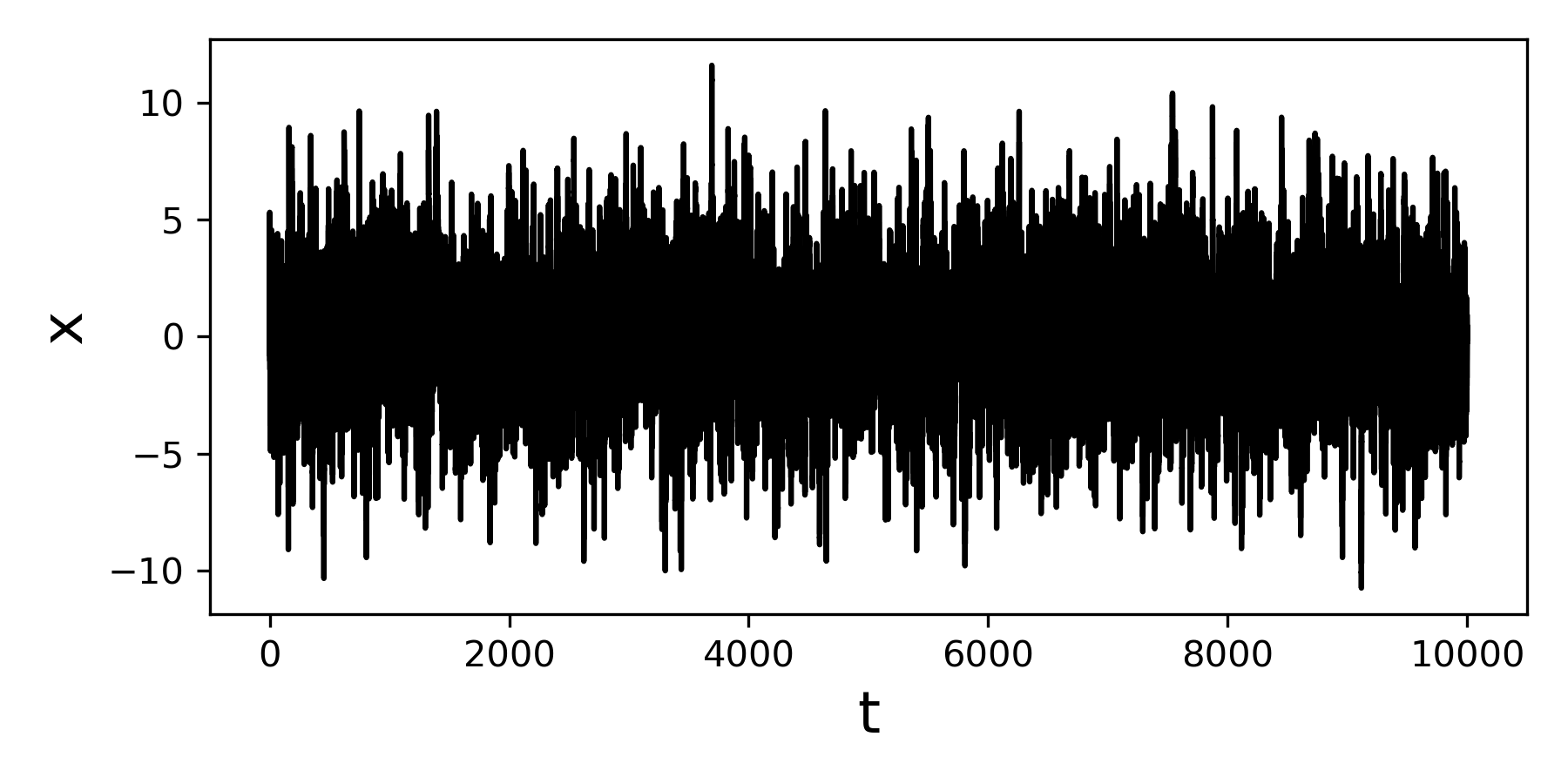
Using jumpdiff to retrieve the parameters¶
Moments and Kramers─Moyal coefficients¶
Take the timeseries X and use the function moments to retrieve the conditional moments of the process.
For now let us focus on the shortest time lag, so we can best approximate the Kramers—Moyal coefficients.
For this case we can simply employ
20 | edges, moments = jd.moments(timeseries = X) |
In the array edges are the limits of our space, and in our array moments are recorded all 6 powers/order of our conditional moments.
Let us take a look at these before we proceed, to get acquainted with them.
We can plot the first moment with any conventional plotter, so lets use here plotly from matplotlib.
To visualise the first moment, simply use
21 22 | import matplotlib.pyplot as plt plt.plot(edges, moments[1]/delta_t) |
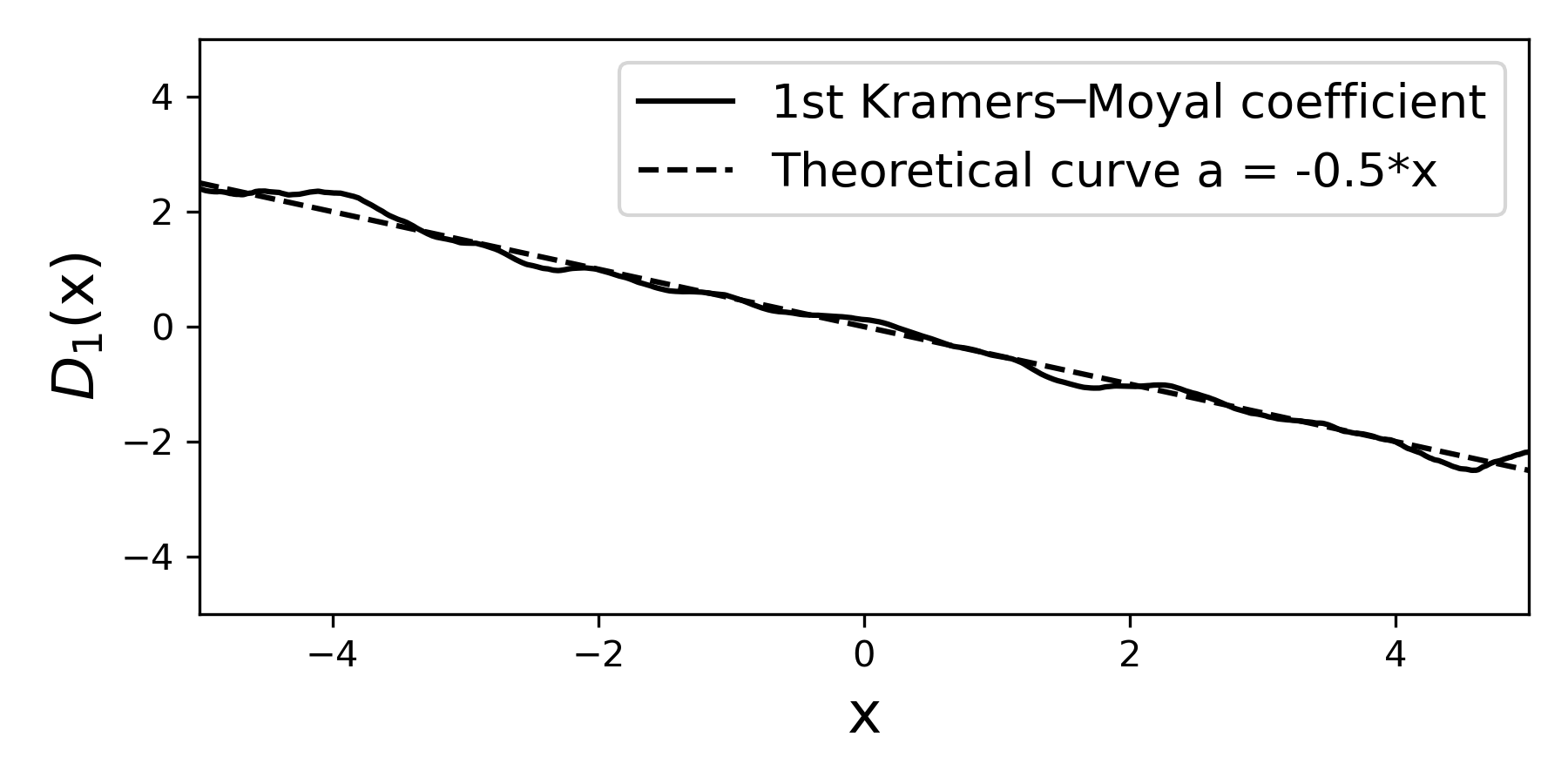
The first moment here (i.e., the first Kramers—Moyal coefficient) is given solely by the drift term that we have selected -0.5*x.
In the plot we have also included the theoretical curve, which we know from having selected the value of a(x) in line 8.
Similarly, we can extract the second moment (i.e., the second Kramers—Moyal coefficient) is a mixture of both the contributions of the diffusive term \(b(x)\) and the jump terms \(\xi\) and \(\lambda\).
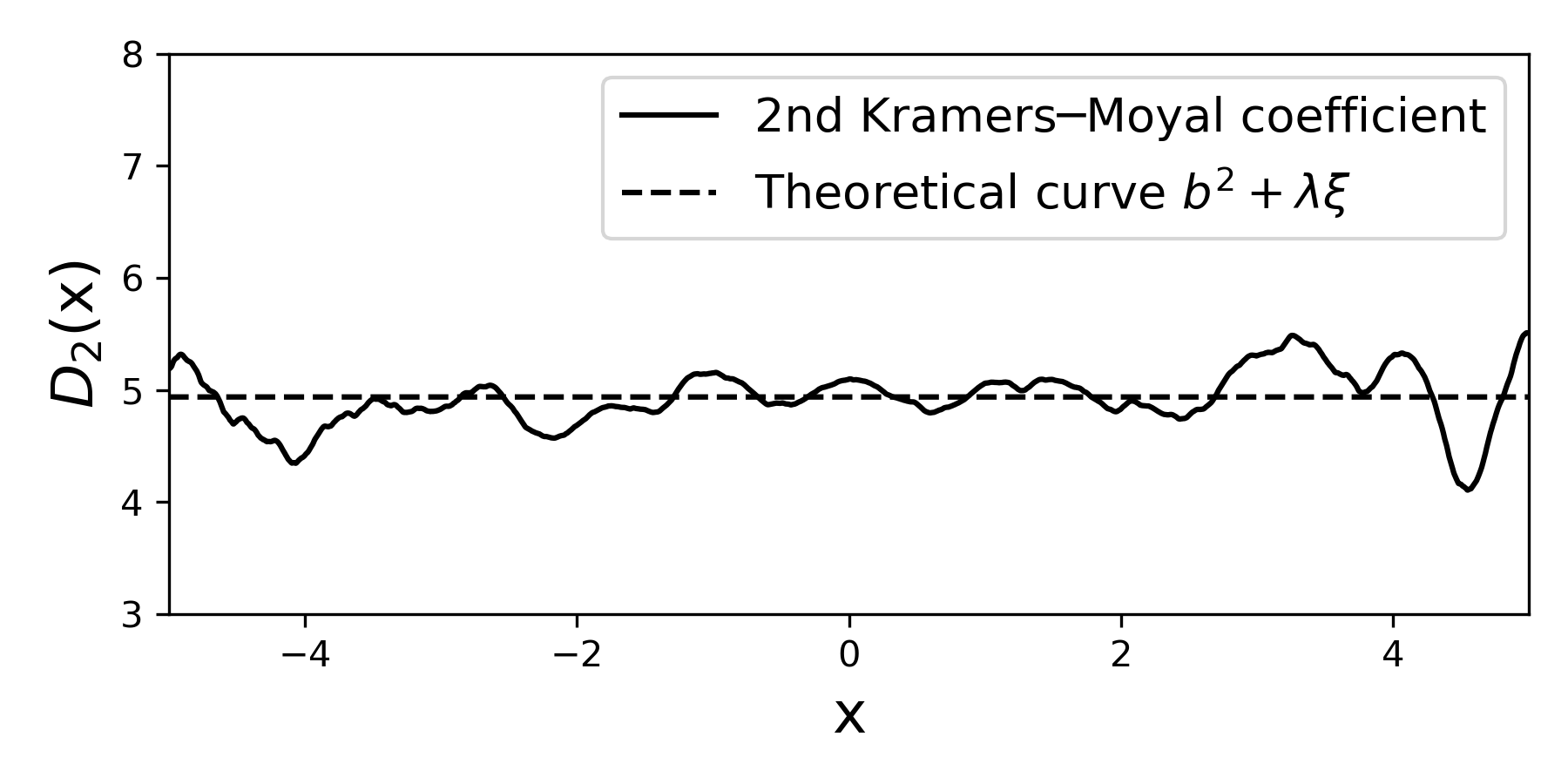
You have this stored in moments[2].
Distinguishing pure diffusions from jump-diffusions¶
One important question when we have some time series – possibly from real-world data – is to be able to discern if this timeseries is a pure diffusion process (a continuous stochastic process) or a jump-diffusion process (a discontinuous stochastic process).
For this, jumpdiff has an easy to use function, called q_ratio.
The idea behind distinguishing continuous and discontinuous processes is simple:
diffusion processes diffuse over time, thus they take time to occupy space; jump-diffusion processes can jump, and thus statistically, they occupy all space very fast.
To analyse this let us design a simple example – with some numerically generated data – that shows the use of q_ratio and how to read it.
Let us generate two trajectories, using jd_process, denoted d_timeseries and j_timeseries, for diffusion timeseries and jumpy timeseries.
Naturally the first must not include a jump term.
To keep it simple, we will use the same parameters for both, expect for the jumps:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | import jumpdiff as jd # integration time and time sampling t_final = 10000 delta_t = 0.01 # Drift function def a(x): return -0.5*x # Diffusion function def b(x): return 0.75 # generate 2 trajectories d_timeseries = jd.jd_process(t_final, delta_t, a=a, b=b, xi=0, lamb=0) j_timeseries = jd.jd_process(t_final, delta_t, a=a, b=b, xi=2.5, lamb=1.75) |
Note how xi and lamb are different for each process
To now examine the rate of diffusion of the processes, we need to generate a time arrow, which we denote lag.
This needs to be a integer list >0.
18 19 | import numpy as np lag = np.logspace(0, 3, 25, dtype=int) |
Lastly we just need to can the q_ratio for our two timeseries
20 21 | d_lag, d_Q = jd.q_ratio(lag, d_timeseries) j_lag, j_Q = jd.q_ratio(lag, j_timeseries) |
And with the help of matplotlib’s plotly, we can visualise the results in a double logarithmic scale
22 23 24 25 | import matplotlib.plotly as plt plt.loglog(d_lag, d_Q, '-', label='diffusion') plt.loglog(j_lag, j_Q, 'o-', label='jump-diffusion') |
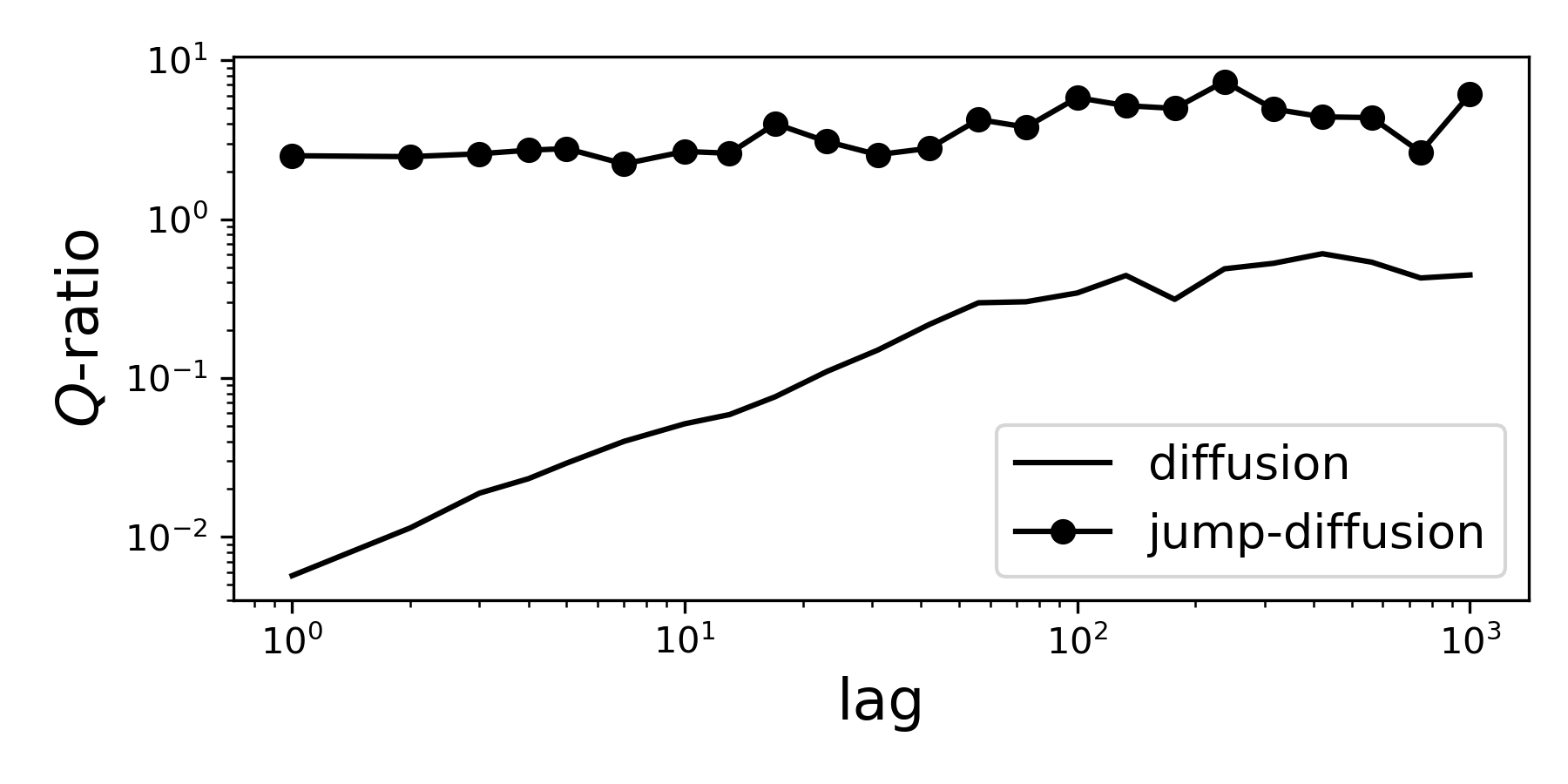
As we can see, the diffusion process grows with our time arrow lag, where the jump-diffusion is constant (does not depend on lag).
Jump processes will show a constant relation with code:lag, where diffusion processes a linear relation.
Table of Content¶
Literature¶
An extensive review on the subject can be found here.
Funding¶
Helmholtz Association Initiative Energy System 2050 - A Contribution of the Research Field Energy and the grant No. VH-NG-1025 and STORM - Stochastics for Time-Space Risk Models project of the Research Council of Norway (RCN) No. 274410.